弊社の論文が去年に引き続き、本年も公益社団法人土木学会の土木学会論文集C（地圏工学）に掲載されました。

■岩田智明　“直線すべりによる新たな土圧算定法”　 　土木学会論文集C（地圏工学）, Vol. 74, No. 1, 34-49, 2018.

 

論文の概要は以下のとおりです。詳細はJ-STAGE（電子ジャーナル）上でご確認ください。

　本論文は擁壁の設計等に用いる土圧（土圧：土から擁壁に、または擁壁から土に生じる力）に関する論文です。当算定法による成果は主に以下の３つです。
　①岩田円を用いた新たな土圧算定法の提案
　②クーロン式とランキン式を従来法に比較して簡単に求めることができる
　③土圧計算式の適用範囲を拡張


　上記の①～③について以下に概要を説明いたします。（ただし、著作権は土木学会に譲渡しているため、詳細な説明は差し控えさせていただきます。）


①岩田円を用いた新たな土圧算定法の提案

　本論文では、クーロン土圧理論やランキン土圧理論の土圧計算法とは異なるアプローチによる、新たな土圧計算法を提案しています。この土圧計算法を用いて土圧計算式を導くことで、既往論文で導いたクーロン土圧理論に基づく土圧計算式と全く同じ計算式が得られます。つまり、このことから、この新たな土圧計算法の妥当性が確認できたといえます。また、この土圧計算法ではモールの応力円を利用した『岩田円』を使用します。
　この土圧計算法の主な利点は、岩田円を利用することで、
　①比較的容易に計算式を導けること
　②すべり角の方向や、ある面に作用する土圧の大きさや方向・すべり角の状態の理解が容易になること
が挙げられます。


②クーロン式とランキン式を従来法に比較して簡単に求めることができる

　擁壁の設計において土圧計算式は、『クーロン式』と『ランキン式』が多く用いられます。これらの土圧計算式では、計算を簡素化するためにすべり面（すべり線）を直線と仮定して、土圧を求められます。現在において、この２つの式は全く異なるものとして使用されています。しかし、クローン土圧理論またはランキン土圧理論と異なる、本提案の土圧理論（土圧計算法）の下では、土をある状態に見立てれば与条件を変えるだけで、これらの式を導くことが可能です。具体的に言えば、これらの計算式は本提案の下では、単に極限状態時での破壊基準が異なるだけなのです。
　従来、クローン式の導出には導関数を必要としていました。しかし、前記の岩田円を用いることで、これをいとも容易く導くことができるようになります。例えば、物部・岡部式（地震時クーロン式）は次のように求めることができます。


＜＜　例　　物部・岡部式の簡単な求め方＞＞
下図のωβRが物部・岡部式でのすべり角に関する数式記号です。つまり、このωβRを求めれば自ずとすべり角の計算式が得られます。

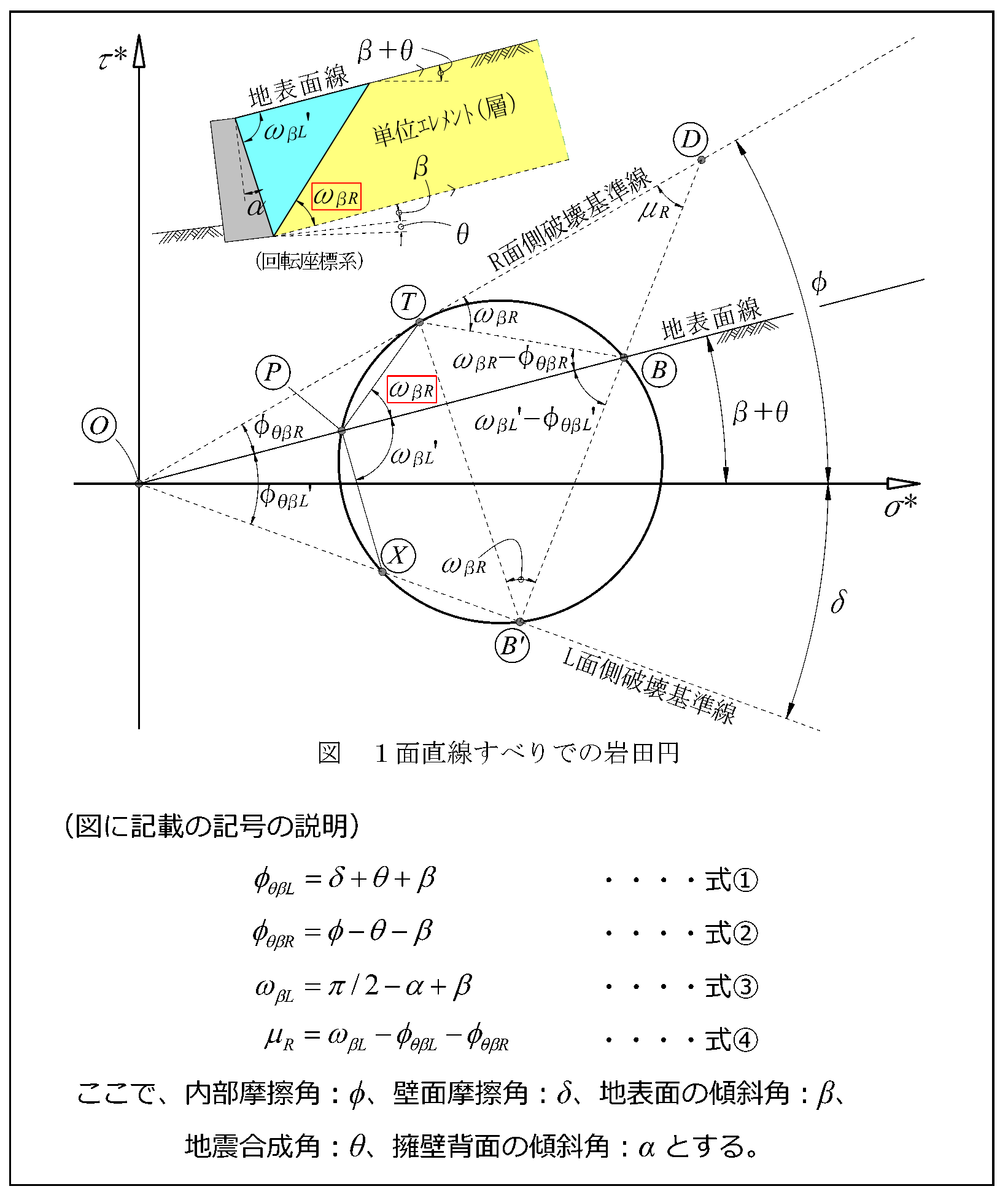
まず、方べきの定理を利用すれば△DBT ∽△DTB ' であるので、正弦定理を用いて整理すれば，DB’/DBは次の式⑤になります。

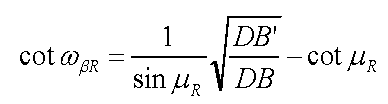・・・・式⑤

ここで、予め、式⑤を次の式⑥に変形しておきます。(加法定理を応用して変形)

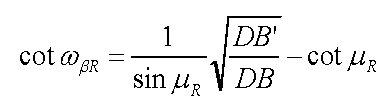・・・・式⑥

図のDBは△OBDに着目し、正弦定理を用いれば次の式⑦になります。

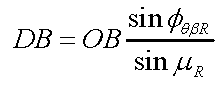・・・・式⑦

また、DB’は、OB'が求まれば△OB’Dに着目し正弦定理を用いてば求めることができるため、まずOB'を求めます。
OB’は△OB’Bに着目し、正弦定理を用いれば次の式⑧となります。

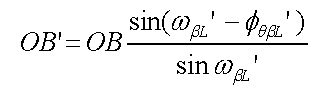・・・・式⑧

よってDB’は、次の式となります。

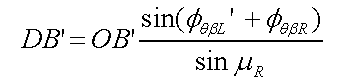・・・・式⑨

したがって、式⑥に、式⑦～⑨と図の式①～④を代入すれば次の式⑩(物部・岡部式)が導かれます。

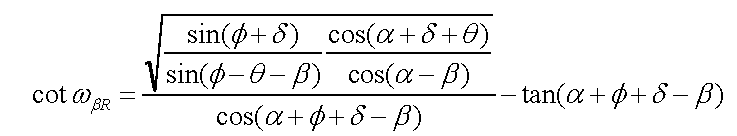・・・・式⑩

 

③土圧計算式の適用範囲を拡張

　新しい土圧計算法では、これまで、土圧を計算できなかった適用条件まで、一部、計算することが可能となりました。それは以下のような状態です。

1.長いかかと版を有する片持ちばり式擁壁の背面が一様な斜面で粘着力を考慮する場合
2.長いかかと版を有する片持ちばり式擁壁の背面が一様な斜面で載荷荷重を考慮する場合

また、地震時ランキン土圧計算式を以下のように、さらに簡略化することに成功しています。

旧（従来の計算式）

 

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

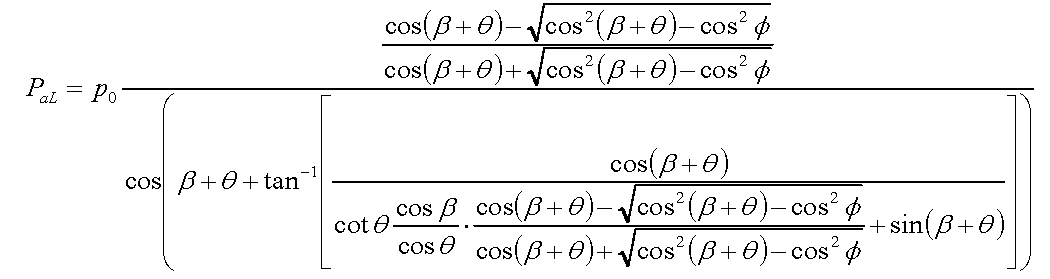
新（岩田によって簡略化された計算式）

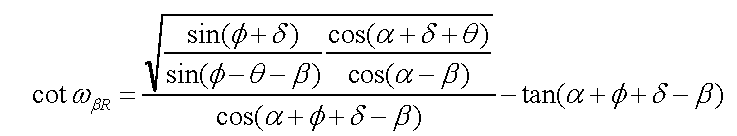
注：p0は岩田の論文をご確認ください

さいごに

　現在で使用されている、クーロン土圧やランキン土圧に用いる主働土圧について、岩田は、『これらの土圧は主働土圧ではなく、真の主働土圧は、岩田の論文に使用されている基準主働土圧Pa0（回転座標系の土圧水平方向成分PaθH）である。』と考えています。岩田の論文を読んでいただけますとご理解いただけますように、現在に使用している主働土圧とは、真の主働土圧がすべり面に作用する土圧に変換されたものです。　水平方向の力が意味を成す理由について、わかりやすい例として水を見本に説明します。水は、ある深さでの鉛直方向の水圧が水平方向に同じ大きさで作用します。これは、鉛直方向の水圧が水平方向の水圧に変換されているためです。同様に土の場合でも同じことが言え、鉛直方向に作用する土の応力は水平方向の応力に変換されます。この変換された応力の合計が主働土圧となります。今後、主働土圧の定義が、この真の主働土圧の定義に変わることを期待しています。（なお、受働土圧についても同様です。）