株式会社ミズキコンサルタント

弊社の論文が公益社団法人土木学会の土木学会論文集C（地圏工学）に掲載されました。

■岩田智明　“現状斜面に対応する新しい土圧計算式”　 　土木学会論文集C（地圏工学）, Vol. 73, No. 2, 195-211, 2017.

概要は以下のとおりです。ご興味をお持ちいただけましたら、土木学会論文集をご購読ください。

　擁壁には、土による、土圧という見えない力が生じます。当論文ではその土圧に関する以下の５項目の成果を挙げています。
　①クーロン式を粘着力が考慮できる計算式への拡張に成功
　②クーロン式を擁壁背面の地形が複雑な地表面形状を呈する場合に対応できる計算式への拡張に成功
　　（①、②の成果により、試行くさび法に代わり得る新たな数式を導出。）
　③改良試行くさび法に代わり得る、2面直線すべり式の収束計算法の提案
　　（ただし、かかと版の長い片持ちばり式擁壁に限る。）
　④地震時ランキン土圧の計算式の簡略化とすべり角の計算式の拡張に成功
　⑤重力式擁壁に作用する土圧は、擁壁背面に想定するすべり形態によって変化することを提唱
　　（現在の擁壁の設計法の問題点を指摘。）


1.土圧計算式であるクーロン式を粘着力が考慮できる計算式への拡張に成功(上記①に関する記述）
　電磁気学の分野においても名声を馳せるクーロン(Charles-Augustin de Coulomb)が37歳の時(1773年)、論文（※1参照）において土圧理論を発表しました。
　現在において、擁壁に作用する土圧は、クーロンの土圧理論を基本として計算されています。
　しかし、240年の間、粘着力（砂のようなサラサラした土ではなく、粘土のような粘りのある土に作用する付着力）を考慮した計算式が未解明のままでした。
当論文では、これを解明し、クーロン式を粘着力が考慮できる計算式への拡張に成功しました。
　※1【Essais sur une application des règles de maximis et minimis à quelques problèmes de statique relatifs à l'architecture】


2.地震時ランキン土圧の計算式の簡略化とすべり角の計算式の拡張に成功（上記③に関する記述）
　半無限斜面における地中内に生じる土圧はランキン土圧によって計算されます。（詳細は論文内をご確認ください。）また、一般的なランキン土圧計算式（地震力を考慮しない計算式）は、多くの土木技術者に知られています。一方、慣性力を考慮するランキン土圧の計算式は、複雑な計算式であるがゆえ、一般化しておらず一部の有知識者しかその存在を知らないのが現状です。さらに、過去（1970年頃）にこの計算式を掲載した専門書はありましたが、現在で、この計算式を掲載する専門書は見当たりませんでした。
当論文では、この重要計算式（地震時ランキン土圧の計算式）の簡略化に成功しています。
また、半無限斜面に重力と慣性力が作用する地中内の極限応力状態（ランキン場とも呼ばれる応力状態）でのすべり角の計算式を地震時モールの応力円を用いて導き出すことに成功しています。


3.擁壁背面の地形が複雑な地表面形状を呈する場合に対応できる計算式を発明
（上記②および④に関する記述）
　これまで、擁壁の背面の地形が複雑な地表面形状となっている場合（例えば、地表面が現状斜面のように一様な勾配となっていない場合）に土圧を計算できる計算式は存在しませんでした。
　当論文では、クーロンの土圧理論を用いて当問題点を解決する計算式を導いています。
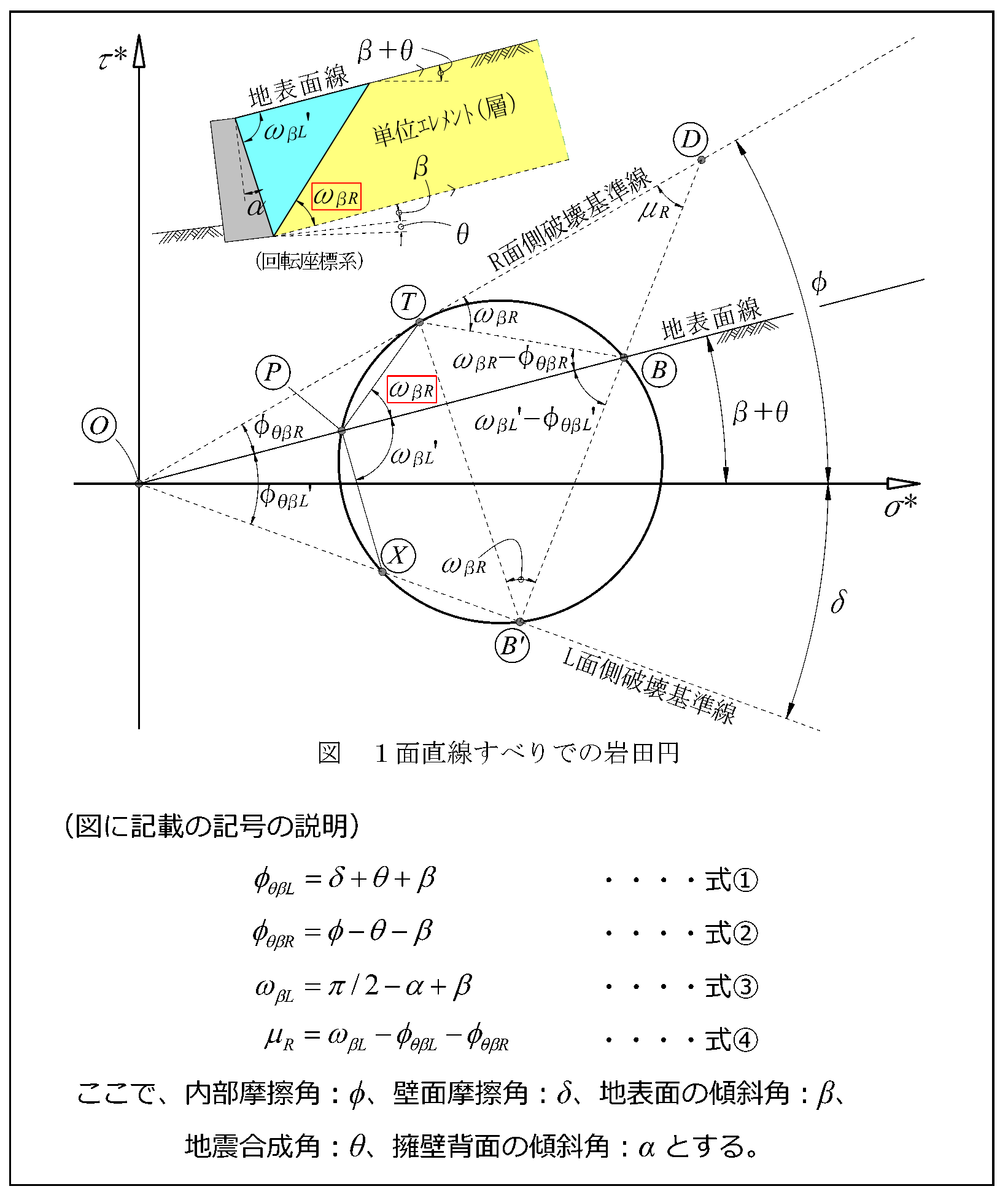
　擁壁背面側に発生するすべり形態には岩田が呼称する『１面直線すべり』と『２面直線すべり』があります。（詳細は論文内をご確認ください。）
『１面直線すべり』のすべり形態（例えば、重力式擁壁の背面に発生するすべり形態）では、従来より土圧計算に用いられてきた試行くさび法を利用することなく、本発明の計算式で直接、土圧を計算することが可能となります。
『２面直線すべり』のすべり形態（例えば、片持ちばり式擁壁の背面に発生するすべり形態）では、収束計算アルゴリズムを用いて土圧計算することで、従来の計算法（改良試行くさび法）に比べて迅速、かつ高精度な解が算出することが可能となりました。(ただし、２つのすべり面が地表面と交差する場合に限ります。)



4.重力式擁壁に作用する土圧は想定するすべり形態によって変化することを提唱（上記⑤に関する記述）
　現在の重力式擁壁に作用する土圧は、前述の『１面直線すべり』のすべり形態によって計算されています。しかし、擁壁の背面勾配が極めて緩勾配となる場合において『１面直線すべり』は発生せず、『２面直線すべり』が発生することは明らかです。
　当論文では、『１面直線すべり』から『２面直線すべり』のすべり形態に変異する限界点を理論的に説明し、擁壁背面に発生するすべり形態によって土圧を評価することを提案しています。

　2018年に弊社が発明した擁壁の計算アルゴリズムについて、特許を出願し、特許を権利化することができました。


　当該特許技術では、擁壁の設計に用いられる土圧について、試行計算を行って最大土圧を算定する従来法に対して、この計算システムを用いることで、直接的に最大土圧を算定することを可能となります。この効果により、土圧算定の際に、従来までの技術者によって異なる解を算出し得るようなファジィ的要素を取り除き、誰もが正確な解を算出できるため、算出解に信頼性が生まれ、品質の高い成果を提供することが可能となります。


　当社が手掛ける擁壁の設計には、取得した擁壁の安定性評価に関する特許技術（擁壁の土圧評価方法、擁壁の安全性評価プログラムおよび安全性評価システム）が使われています。


　なお、特許技術の詳しい内容については、以下からご覧いただけます。ご興味のある方は、どうぞご閲覧ください。


↓下をクリックして記事をご覧ください。

独立行政法人　工業所有権情報・研修館（INPIT）の知財総合支援窓口のHPで全国の企業様の支援事例が掲載されている中で、株式会社ミズキコンサルタントが紹介されました。


導入への課題となっていたことや、取り組みの成果などが載せられています。
↓下をクリックして記事をご覧ください。

弊社の論文が去年に引き続き、本年も公益社団法人土木学会の土木学会論文集C（地圏工学）に掲載されました。

■岩田智明　“直線すべりによる新たな土圧算定法”　 　土木学会論文集C（地圏工学）, Vol. 74, No. 1, 34-49, 2018.

 

論文の概要は以下のとおりです。詳細はJ-STAGE（電子ジャーナル）上でご確認ください。

　本論文は擁壁の設計等に用いる土圧（土圧：土から擁壁に、または擁壁から土に生じる力）に関する論文です。当算定法による成果は主に以下の３つです。
　①岩田円を用いた新たな土圧算定法の提案
　②クーロン式とランキン式を従来法に比較して簡単に求めることができる
　③土圧計算式の適用範囲を拡張


　上記の①～③について以下に概要を説明いたします。（ただし、著作権は土木学会に譲渡しているため、詳細な説明は差し控えさせていただきます。）


①岩田円を用いた新たな土圧算定法の提案

　本論文では、クーロン土圧理論やランキン土圧理論の土圧計算法とは異なるアプローチによる、新たな土圧計算法を提案しています。この土圧計算法を用いて土圧計算式を導くことで、既往論文で導いたクーロン土圧理論に基づく土圧計算式と全く同じ計算式が得られます。つまり、このことから、この新たな土圧計算法の妥当性が確認できたといえます。また、この土圧計算法ではモールの応力円を利用した『岩田円』を使用します。
　この土圧計算法の主な利点は、岩田円を利用することで、
　①比較的容易に計算式を導けること
　②すべり角の方向や、ある面に作用する土圧の大きさや方向・すべり角の状態の理解が容易になること
が挙げられます。


②クーロン式とランキン式を従来法に比較して簡単に求めることができる

　擁壁の設計において土圧計算式は、『クーロン式』と『ランキン式』が多く用いられます。これらの土圧計算式では、計算を簡素化するためにすべり面（すべり線）を直線と仮定して、土圧を求められます。現在において、この２つの式は全く異なるものとして使用されています。しかし、クローン土圧理論またはランキン土圧理論と異なる、本提案の土圧理論（土圧計算法）の下では、土をある状態に見立てれば与条件を変えるだけで、これらの式を導くことが可能です。具体的に言えば、これらの計算式は本提案の下では、単に極限状態時での破壊基準が異なるだけなのです。
　従来、クローン式の導出には導関数を必要としていました。しかし、前記の岩田円を用いることで、これをいとも容易く導くことができるようになります。例えば、物部・岡部式（地震時クーロン式）は次のように求めることができます。


＜＜　例　　物部・岡部式の簡単な求め方＞＞
下図のωβRが物部・岡部式でのすべり角に関する数式記号です。つまり、このωβRを求めれば自ずとすべり角の計算式が得られます。

まず、方べきの定理を利用すれば△DBT ∽△DTB ' であるので、正弦定理を用いて整理すれば，DB’/DBは次の式⑤になります。

・・・・式⑤

ここで、予め、式⑤を次の式⑥に変形しておきます。(加法定理を応用して変形)

・・・・式⑥

図のDBは△OBDに着目し、正弦定理を用いれば次の式⑦になります。

・・・・式⑦

また、DB’は、OB'が求まれば△OB’Dに着目し正弦定理を用いてば求めることができるため、まずOB'を求めます。
OB’は△OB’Bに着目し、正弦定理を用いれば次の式⑧となります。

・・・・式⑧

よってDB’は、次の式となります。

・・・・式⑨

したがって、式⑥に、式⑦～⑨と図の式①～④を代入すれば次の式⑩(物部・岡部式)が導かれます。

・・・・式⑩

 

③土圧計算式の適用範囲を拡張

　新しい土圧計算法では、これまで、土圧を計算できなかった適用条件まで、一部、計算することが可能となりました。それは以下のような状態です。

1.長いかかと版を有する片持ちばり式擁壁の背面が一様な斜面で粘着力を考慮する場合
2.長いかかと版を有する片持ちばり式擁壁の背面が一様な斜面で載荷荷重を考慮する場合

また、地震時ランキン土圧計算式を以下のように、さらに簡略化することに成功しています。

旧（従来の計算式）

 

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓

新（岩田によって簡略化された計算式）

注：p0は岩田の論文をご確認ください

さいごに

　現在で使用されている、クーロン土圧やランキン土圧に用いる主働土圧について、岩田は、『これらの土圧は主働土圧ではなく、真の主働土圧は、岩田の論文に使用されている基準主働土圧Pa0（回転座標系の土圧水平方向成分PaθH）である。』と考えています。岩田の論文を読んでいただけますとご理解いただけますように、現在に使用している主働土圧とは、真の主働土圧がすべり面に作用する土圧に変換されたものです。　水平方向の力が意味を成す理由について、わかりやすい例として水を見本に説明します。水は、ある深さでの鉛直方向の水圧が水平方向に同じ大きさで作用します。これは、鉛直方向の水圧が水平方向の水圧に変換されているためです。同様に土の場合でも同じことが言え、鉛直方向に作用する土の応力は水平方向の応力に変換されます。この変換された応力の合計が主働土圧となります。今後、主働土圧の定義が、この真の主働土圧の定義に変わることを期待しています。（なお、受働土圧についても同様です。）

愛媛県建設産業経営革新等助成事業の支援対象に選ばれました。

・事業内容
　自社考案の特許技術「擁壁安定性評価システム」を用いた新たなソフトウェアの開発と、そのソフトウェアがオンライン上において低コストで利用できるサービスを提供することにより経営基盤の強化を図る。
↓下をクリックして記事をご覧ください。